Eine möglichst hohe Schärfe ist bei allen Schneidwerkzeugen wünschenswert, ebenso bei Klingenwaffen. Während Werkzeuge im Allgemeinen in definierten Situationen eingesetzt und daraufhin optimiert werden, sind die Anforderungen an Klingenwaffen, besonders an solche mit längere Klingen, oft widersprüchlich. Um die verschiedenen Einflüsse auf die Schärfe einer Klinge und die damit einhergehenden Effekte und notwendigen konstruktiven Kompromisse geht es in dieser Arbeit.
Faktoren der Schärfe
Obwohl der Begriff der Schärfe im Alltag gebräuchlich ist, gibt es keine einheitliche Definition. Es liegt jedoch nahe, dass eine Klinge als umso schärfer angesehen wird, je weniger Kraft ausgeübt werden muss, um einen Schnitt in einem bestimmten Material zu verursachen oder je tiefer der Schnitt mit einer bestimmten Kraft ist. Gleichzeitig soll die Klinge nicht nur scharf, sondern auch schnitthaltig sein, d. h. die Schneide soll vielen Schnittvorgängen standhalten können, ohne ihre Schärfe nennenswert zu verlieren. Darüber hinaus ist es von Vorteil – insbesondere beim Fechten –, wenn die Klinge auch anderen Belastungen als denen des idealen Schneidvorgangs standhält. Je nach Anwendung muss der jeweils optimale Kompromiss aus Schärfe und Robustheit neu gefunden werden. [1, 2]
Mehrere Faktoren beeinflussen die Schärfe einer Klinge, darunter die Eigenschaften des verwendeten Stahls, die Bewegung von Klinge und Ziel, die Krümmung der Klinge, der Schneidenwinkel, der Schliff und die Politur.
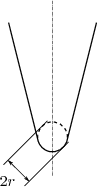
Schneidenradius und Politur
McCarthy et al. [3] ermittelten die Abhängigkeit der zur Schnittbildung nötigen Kraft \(F\) vom endlichen Schneidenradius \(r\) und fanden einen proportionalen Zusammenhang: \begin{equation} F \sim r \label{eq1} \end{equation} Mit der Proportionalität der Schneidenfläche zum Schneidenradius \(r\) passt das Ergebnis zum von Szabo et al. [4] festgestellten proportionalen Zusammenhang von Kraft und Schneidenfläche. Der Schneidenradius \(r\), siehe Abb. 1, liegt typischerweise im Bereich von wenigen Mikrometern. Mit bloßem Auge lässt sich dieser Faktor der Klingenschärfe also i. A. nicht beurteilen.
Die Politur der Schneide wirkt sich auf zwei Wegen auf die Schärfe der Klinge aus. Zum einen hat eine feinere Politur der Schneidflächen eine feinere Schneide mit geringerem Schneidenradius \(r\) und weniger Defekten zur Folge. Zum anderen bewirkt eine feinere Politur eine glattere Oberfläche der Schneide, was den Reibungswiderstand beim Schnitt verringert. Einen solchen Effekt erzielt man auch durch Beschichtungen z. B. mit amorphem Kohlenstoff bei Rasierklingen [2], wobei zu berücksichtigen ist, dass bei den meisten Materialen nur die Reibung an der Wate nennenswert zum gesamten Reibungswiderstand beiträgt, wo die Beschichtung beim Nachschärfen abgetragen würde. McGorry et al. [5] untersuchten den Einfluss der Klingenpolitur auf den Kraftaufwand bei verschiedenen Schnittvorgänge bei der Schlachtung von Lämmern. Während der Kraftaufwand bei langen Schnitten durch verschiedene Arten von Gewebe bei feinerer Politur signifikant geringer war, hatte die Politur tendenziell denselben Einfluss auf die kurzen Schnitte durch Muskelfleisch, jedoch unterhalb des Signifikanzniveaus. Landes [2] führt aus, dass bei ziehenden Schnitten eine sägeartige Schartigkeit der Klinge das Durchtrennen begünstigen kann, so dass die Auswirkungen der Schneidenbehandlung je nach Ausführung des Schnitts variieren können.
Schneidenwinkel, Ein- und Zweischneidigkeit
Der Schneidenwinkel ist der Winkel, unter dem sich die Ebenen der Schneiden bzw. deren Tangentialebenen schneiden. Marsot et al. [1] ermittelten unter Laborbedingungen die Kraft \(F\), mit der ein Ausbeinmesser ein fleischähnliches Substrat schneidet, bei Schneidenwinkeln \(\varepsilon\) von 27°, 30°, 35° und 40° und kamen zu dem Ergebnis, dass die Kraft \(F\) proportional zum Tangens des halben Schneidenwinkels ist: \begin{equation} F \sim \tan{\frac{\varepsilon}{2}} \label{eq2} \end{equation} Zu diesem Zusammenhang kommen auch Arcona und Dow [6] für das Zerteilen von Kunststofffilmen mit Schneidenwinkeln unter 45°. McCarthy et al. [3] stellen mit Hilfe eines Finite-Elemente-Methode-Modells einen bilinearen Zusammenhang her zwischen der Kraft \(F\), die einen Schnitt in einem Polyurethan-Substrat verursacht und dem Schneidenwinkel \(\varepsilon\). Jedoch beschreibt hier auch Gleichung (2) die Resultate hinreichend genau, siehe Abb. 3. Neben der Schärfe untersuchten Marsot et al. [1] auch die Bedeutung des Schneidenwinkels und des verwendeten Klingenstahls auf die Schnitthaltigkeit mit dem plausiblen Resultat, dass ein größerer Schneidenwinkel eine größere Schnitthaltigkeit bedingt.
McGorry et al. [5] untersuchten unter Realbedingungen den Einfluss der Schneidenwinkel 20°, 30° und 45° auf die Kraft, die zum Zerteilen von Fleisch nötig ist. Aus ihren Messungen folgern sie, dass der Schneidenwinkel im untersuchten Bereich keinen signifikanten Einfluss auf die zum Zerteilen nötige Kraft hat. Das legt nahe, dass der die Schärfe mindernde Effekt der größeren Schneidenwinkel in der Praxis von anderen Effekten überlagert wird. Auch McCarthy et al. [3] beschreiben die Bedeutung des Schneidenwinkels als gering gegenüber anderen Einflüssen auf die Schärfe.

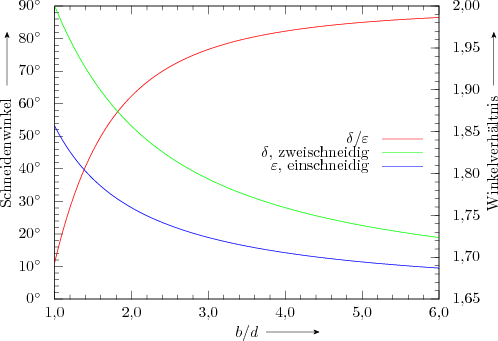
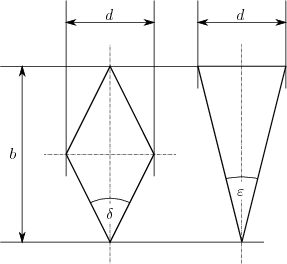
Aus den Gleichungen (6) und (7) sowie aus Abb. 4 ist zu erkennen, dass bei demselben Verhältnis von Klingenbreite und -dicke der Schneidenwinkel \(\delta\) einer zweischneidigen Klinge mit rhombischem Querschnitt 1,69- bis 2-mal so groß ist wie der Schneidenwinkel \(\varepsilon\) einer einschneidigen Klinge mit dreieckigem Querschnitt. Mit Gleichung (2) folgt, dass die zum Zerteilen nötige Kraft bei einer zweischneidigen Klinge doppelt so groß ist wie bei einer einschneidigen Klinge mit demselben Verhältnis von Breite zu Dicke.
Stahl
Klingen mit denselben geometrischen Eigenschaften, aber unterschiedlichen Legierungen und Härten wurden von Marsot et al. verglichen. [1] Hierbei wurden Ausbeinmesser mit Klingen aus X46Cr13 (1.4034) mit einer Härte von 54(1) HRC, aus X50CrMoV15 (1.4116) mit 56(1) HRC und aus X70CrMo15 (1.4109) mit 57(1) HRC verwendet. Es stellte sich heraus, dass der Stahl keinen Einfluss auf die anfänglich nötige Schneidkraft hat, dass jedoch bei weicheren Stählen die zum Schneiden nötige Kraft mit der Häufigkeit der Verwendung schneller steigt als bei härteren Stählen.
Im Kontext der Anwendung auf Schwerter ist bei diesem Ergebnis zu berücksichtigen, dass die von Marsot et al. untersuchten Stähle allesamt rostfreie Stähle sind, die für die Verwendung in Schwertklingen wegen ihrer geringeren Zähigkeit ungeeignet sind. Landes [2] erklärt, dass je nach Stahl verschiedene mikroskopische Schneidengeometrien möglich oder unmöglich sind. So eignen sich sprödere Stähle mit höheren Anteilen an großen Carbidphasen nicht für Schneiden mit geringem Schneidenradius \(r\), da eine zu schmale Schneide bereits beim Schleifen der Schneide abreißt, woraus sich für sprödere Stähle eine höhere minimale Breite der Schneide ergibt. Geringere Schneidenradii lassen sich demnach nur mit duktileren Stählen erreichen.
Der Stahl und dessen Wärmebehandlung wirken sich nicht nur auf die Schneide einer Klinge aus, sondern auch auf andere Eigenschaften, die beim Fechten eine Rolle spielen. So führt eine zu harte und spröde Klinge zu einer geringeren Schlagzähigkeit und damit zu einer höheren Bruchgefahr. Zwar lässt sich die höhere Bruchgefahr durch eine dickere Klinge ausgleichen, die jedoch zu einer veränderten Masse und Masseverteilung führt. Während sich sowohl die erhöhte Sprödigkeit als auch die andere Masseverteilung bei kürzeren Klingen nur wenig auf die Handhabung auswirken, können solche Veränderungen bei längeren Klingen wie beim langen Schwert dazu führen, dass sie unbrauchbar brüchig bzw. unbrauchbar träge werden.
Schneidende Komponente und Klingenkrümmung
Atkins [7] untersuchte den Einfluss der Klingenkrümmung auf die zum Schneiden weicher Materialen nötige Kraft. Er führt aus, dass sich die Klingenkrümmung über das Verhältnis \(\xi\) der Klingengeschwindigkeit entlang der Schneide zur Klingengeschwindigkeit senkrecht zur Schneide auf die während des Schnitts auf das Material wirkende Kraft auswirkt. Generell verringert eine höhere slice/push ratio \(\xi\) die senkrecht zur Klinge wirkende Kraft unabhängig von den mikroskopischen Eigenschaften der Schneide, was nicht nur den Kraftaufwand reduziert, sondern wie beim Zerteilen von Lebensmitteln oder in der Mikrotomie auch die Qualität des Schnitts erhöht. Praktisch sind der tangentialen Geschwindigkeit jedoch Grenzen gesetzt [7, 8], insbesondere bei manueller Klingenführung wie beim Fechten. Die slice/push ratio \(\xi\) hängt außer von der Klingenkrümmung und den Geschwindigkeiten der Klinge und des Ziels auch vom Winkel der Schneide gegen die Oberfläche des Ziels ab. Neben der Anpassung der Klingenkrümmung für eine bestimmte Bewegung ist auch die Anpassung der Bewegung an eine gegebene Krümmung denkbar. [7]
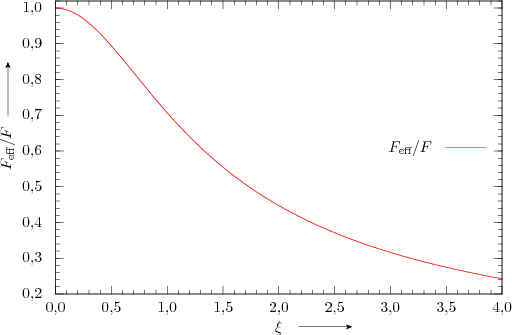
Landes [2] geht qualitativ ebenfalls auf die Bedeutung der slice/push ratio \(\xi\) ein und erklärt den geringeren Kraftaufwand geometrisch durch einen verringerten effektiven Schneidenwinkel \(\varepsilon_\text{eff}\). In seiner Darstellung ergibt sich der effektive Schneidenwinkel \(\varepsilon_\text{eff}\) als Projektion des Schneidenwinkels \(\varepsilon\) in eine zur Schnittebene senkrecht stehenden und zum Vektor der Schnittrichtung parallelen Ebene. Daraus ergibt sich für den effektiven Schneidenwinkel \(\varepsilon_\text{eff}\): \begin{equation} \frac{\tan(\varepsilon_\text{eff}/2)}{\tan(\varepsilon/2)} = \left(1+\xi^2\right)^{-\frac{1}{2}} \end{equation} Mit Gleichung (2) folgt damit für die zum Schneiden effektiv notwendige Kraft \(F_\text{eff}\): \begin{equation} \frac{F_\text{eff}}{F} = \left(1+\xi^2\right)^{-\frac{1}{2}} \end{equation} Zu diesem Ergebnis kommen auch Atkins et al. [8] für den Fall des reibungsfreien Schnitts. Die Abhängigkeit der nötigen Kraft von \(\xi\) ist in Abb. 5 dargestellt.
Zusammenfassung
Die Schärfe wird von verschiedenen Eigenschaften einer Klinge bestimmt. Der verwendete Klingenstahl und seine Wärmebehandlung erlauben unterschiedlich feine Schneiden und geben den sinnvollen Bereich für Schneidenwinkel vor. Bei einem Schwert muss bedacht werden, dass der verwendete Stahl ausreichend zäh sein muss, um auch bei Kontakt mit harten Zielen nicht zu brechen. Ebenso muss der Schneidenwinkel ausreichend groß sein, um einen zu schnellen Verschleiß der Schneide unter den typischerweise ungünstigen Bedingungen eines Kampfes zu verhindern. Der notwendigerweise duktile Stahl einer für Kontakt ausgelegten Schwertklinge erlaubt einen Schliff auf geringe Schneidenflächen. Einge geringe Schneidenfläche wird als für die Schärfe wichtigerer Faktor bewertet als der Schneidenwinkel. [1, 3, 5]
Neben den Eigenschaften der Klinge spielt auch die Führung der Klinge eine Rolle für ihre Schärfe. Aus der Bewegung der Klinge, ihrer Neigung zum Ziel und aus ihrer Krümmung ergibt sich die slice/push ratio \(\xi\). Prinzipiell verringert eine höhere slice/push ratio \(\xi\) die zum Schnitt nötige Kraft [8], jedoch sind der schneidenden Komponente sowohl bei der manuellen Klingenführung als auch bei der für eine kampftaugliche Klinge sinnvollen Krümmung praktische Grenzen gesetzt. [7]
Literatur
- [1] J. Marsot, L. Claudon und M. Jacqmin. Assessment of knife sharpness by means of a cutting force measuring system. In: Applied Ergonomics 38.1 (2007), S. 83–89. DOI: 10.1016/j.apergo.2005.12.007.
- [2] R. Landes. Messerklingen und Stahl. 2. Aufl. Bad Aibling: Wieland Verlag, 2006.
- [3] C. T. McCarthy, A. Ní Annaidh und M. D. Gilchrist. On the sharpness of straight edge blades in cutting soft solids: Part II – Analysis of blade geometry. In: Engineering Fracture Mechanics 77.3 (2010), S. 437–451. DOI: 10.1016/j.engfracmech.2009.10.003.
- [4] R. L. Szabo, R. G. Radwin und C. J. Henderson. The influence of knife sharpness on poultry processing operator exertions and the effectiveness of re-sharpening. In: Proceedings of the Human Factors and Ergonomics Society Annual Meeting 42.12 (1998), S. 921–925. DOI: 10.1177/154193129804201218.
- [5] R. W. McGorry, P. C. Dowd und P. G. Dempsey. The effect of blade finish and blade edge angle on forces used in meat cutting operations. In: Applied Ergonomics 36.1 (2005), S. 71–77. DOI: 10.1016/j.apergo.2004.08.002.
- [6] C. Arcona und T. A. Dow. The role of knife sharpness in the slitting of plastic films. In: Journal of Materials Science 31.5 (1996), S. 1327–1334. DOI: 10.1007/BF00353113.
- [7] A. G. Atkins. Optimum blade configurations for the cutting of soft solids. In: Engineering Fracture Mechanics 73.16 (2006), S. 2523–2531. DOI: 10.1016/j.engfracmech.2006.06.006.
- [8] A. G. Atkins, X. Xu und G. Jeronimidis. Cutting, by ‘pressing and slicing,’ of thin floppy slices of materials illustrated by experiments on cheddar cheese and salami. In: Journal of Materials Science 39.8 (2004), S. 2761–2766. DOI: 10.1023/B:JMSC.0000021451.17182.86.
Dieser Text des Autorenkollektivs Tremonia Fechten steht unter
einer Creative Commons Namensnennung 4.0 International Lizenz
